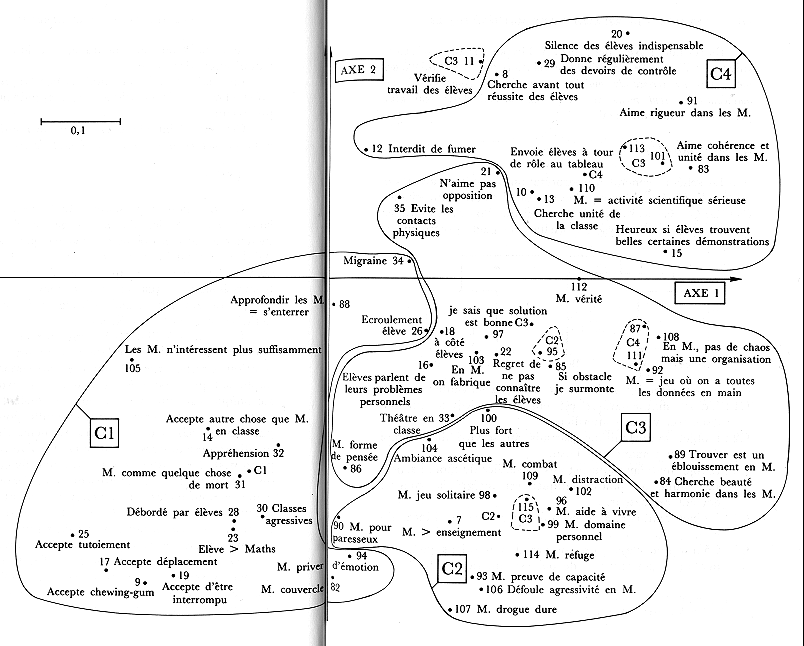
On pourra ,
grâce aux valeurs des catégories C1;
C2; C3; C4, que l'on a trouvées pour soi par
le questionnaire, voir dans quelle mesure on
appartient à telle ou telle
catégorie, évidemment souvent
plusieurs ! IM
Catégorie
C1
Ce qui paraît caractériser cet
ensemble de questions, c'est déjà
une représentation assez négative
des mathématiques. Elles sont
vécues comme un objet qui «prive
d'émotions personnelles » (q. 94) et
d'une « vie affective normale » (q. 82),
plus profondément comme un mauvais objet,
« quelque chose de mort » (q. 31),
pouvant apporter avec lui la mort (affective) :
« Si j'approfondis les mathématiques,
il me semble que je creuse un trou et que je
m'enterre. » (q. 88.) On comprend que ces
professeurs ne sont plus suffisamment
intéressés par les
mathématiques (q. 105) et qu'ils
préfèrent le rapport avec les
élèves à leur enseignement
(q.23).
Cette représentation des
mathématiques peut provenir, en partie au
moins, d'une projection du professeur sur cette
discipline qui, en elle-même, n'est ni
vivante, ni morte. Ce même mécanisme
peut expliquer, me semble-t-il, l'attitude
ambivalente vis-à-vis des
élèves qui ressort des questions
regroupées dans cette classe. En effet, les
questions traduisent un désir de «
rapport » avec les élèves (q.
23), une acceptation de leurs attitudes (q. 25 - 17
- 9 - 19), mais aussi une anxiété
à leur égard, « impression
d'être débordé » par eux
(q. 28), « appréhension » en
entrant dans la classe (q. 32),
anxiété pouvant se traduire
également sous une forme psychosomatique (q.
34).
La projection sur les élèves
peut ainsi être soit la même que sur
les mathématiques, soit celle du
désir de libération de ce mauvais
objet. Le professeur donne aux élèves
la liberté qu'il voudrait pour
lui-même. On peut également
interpréter les questions 26 et 30 comme des
projections.
Il semble ainsi possible de
présenter, après l'étude de
cet ensemble de questions, un mode particulier
de relation avec les mathématiques qui est
celui de protéger le sujet contre une
angoisse persécutrice. En effet, dans la
mesure où l'objet persécuteur interne
pourra être par projection situé
à l'extérieur du sujet sur un objet
précis et limité, ce sujet pourra
ressentir un certain soulagement dans d'autres
domaines.
Ceci peut permettre au sujet de se
défendre en cherchant à
maîtriser cet objet
extériorisé. Cette projection est
déjà une défense qui peut
aussi se prolonger dans une lutte et un combat
imaginaires contre les mathématiques qui
aboutissent à une « victoire » sur
le persécuteur. Ce sentiment de «
victoire » est très souvent
rencontré dans le vécu des
élèves comme dans celui des
professeurs. Un autre moyen utilisé est
celui d'un apparent désinvestissement de cet
objet ; souvent, tel professeur dit que les
mathématiques ne l'intéressent plus,
mais il ne va pas jusqu'à envisager de ne
plus en faire.
L'attitude de certains professeurs
à l'égard des élèves
n'est pas toujours la projection de leur besoin de
liberté, ni un laisser-faire qui peut
aboutir à «l'impression d'être
débordé » (q. 28). Au contraire,
elle peut parfois résulter de la pulsion
d'agressivité elle-même qui se
manifeste alors par une recherche de
maîtrise de la classe. Le
persécuteur n'est plus seulement les
mathématiques, mais il se manifeste aussi
dans l'attitude des élèves en classe
: « Il m'est arrivé de sentir
certaines classes très agressives à
mon égard. » (q. 30.) « Les objets
idéaux et les persécuteurs
introjectés pendant la position
paranoïde-schizoïde forment les
premières racines du sur-moi. »
(Ségal) C'est pourquoi je pense qu'ici les
mathématiques sont au service du sur-moi,
mais non pas comme dans la classe C2 pour forger un
sur-moi plus tolérant et plus supportable ou
pour restaurer le narcissisme du sujet, mais pour
limiter, circonscrire et extérioriser
l'aspect persécuteur du sur-moi.
Actuellement, l'objet mathématique
n'est-il pas souvent vécu socialement comme
persécuteur? Cet objet qui «
sélectionne », qui « empêche
de faire le métier souhaité »,
qui « oblige à un travail non
désiré », etc. oblige le
professeur qui, socialement, en a la charge, le
professeur de mathématiques, à se
situer par rapport à ce fantasme
collectif.
Un professeur représentatif du
groupe C 1 introjectera d'autant mieux cet aspect
social qu'il vivra lui-même les
mathématiques comme persécutrices et
qu'il cherchera alors, pour rétablir un
narcissisme atteint parce qu'il se sent le
représentant des mathématiques par
exemple, à « limiter les
dégâts ». (Voir:
Entretien
de Claire )
Certains professeurs sont ainsi en conflit
apparent avec les mathématiques. Ils
dénoncent très fortement la
persécution des mathématiques mais
s'en font en même temps l'instrument, comme
s'ils avaient besoin justement de cet objet
persécuteur à dénoncer. Ils
peuvent trouver dans cette lutte et cette
dénonciation un soulagement à la
persécution interne de leur propre sur-moi.
Ce soulagement est d'autant plus fort que cette
attitude trouve un écho dans le milieu
social environnant. Il n'est donc peut-être
pas étonnant qu'il soit si difficile de
mettre en doute ou seulement de nuancer de telles
visions des choses. Catégorie
C2
Ce qui caractérise les sujets de
cette classe, c'est une certaine perte
d'investissement du réel.
La relation avec leurs élèves
et avec leurs collègues est difficile (le
centre de gravité de la classe C2 a
l'abscisse la plus élevée sur l'axe 3
— (tendance à l'isolement). Ils se
sentent bien lorsqu'ils sont dans un « domaine
personnel » (q. 99), dans une ambiance
ascétique (q. 104) ou lorsqu'ils sont
solitaires (q. 98).
D'où vient cette perte partielle de
contact avec la réalité ?
Ainsi, ceux qui répondent
affirmativement à ces questions manifestent
un désir d'isolement qui leur permet
d'éviter les tentations d'agressivité
et les blessures narcissiques. Que demandent alors
ces sujets aux mathématiques ?
Ces sujets demandent aux
mathématiques de remplir deux fonctions.
D'une part, participer au refoulement de ces
tendances non acceptées, d'autre part, leur
procurer dans l'imaginaire un objet avec lequel ils
puissent suppléer à leur
insatisfaction.
Grâce aux mathématiques, ces
sujets vont pouvoir « défouler leur
agressivité en toute sécurité
» (q. 106), c'est-à-dire sans
culpabilité ; c'est pourquoi ils
considèrent les mathématiques comme
« un obstacle sportif, un combat, la violence
sous forme de jeu » (q. 109). Ils demandent
aussi aux mathématiques de combler leur
blessure narcissique en leur permettant de «
se sentir plus forts que les autres » (q. 100)
et de se « prouver qu'ils sont capables de
faire quelque chose » (q. 93).
On conçoit alors fort bien que, pour
ces sujets, les mathématiques puissent
remplir des fonctions indispensables : «
Heureusement qu'il y a les mathématiques,
elles m'aident à vivre » (q. 96) et
que, à cause de leurs difficultés de
contact, ils déclarent : « Faire des
mathématiques m'intéresse plus que de
les enseigner. » (q. 7.)
Les plus conscients sentent qu'ils sont
à une certaine distance du réel quand
ils font des mathématiques. Ces
dernières sont alors vécues comme
« vacances » (q. 102) ou comme «
refuge contre les ennuis » (q.
114).
J'interpréterai ainsi cette
description : ces sujets font jouer aux
mathématiques le rôle d'un objet
externe, projection de leur sur-moi. Objet
extérieur à eux-mêmes ; et
à cause de cela, objet qui leur permet de
rester en contact avec un aspect de la
réalité mesurable, quantifiable, qui
sait à la fois résister et être
malléable et par conséquent
acceptable, qui sait dire « non », mais
qui ne fait pas de reproches, comme sans doute leur
propre sur-moi. Un sur-moi exigeant mais
tolérant.
On trouve ici toute la distance qu'il y a
entre la réponse « ce n'est pas cela
» donnée par une calculatrice à
un élève qui a trouvé un
résultat inexact et le « tu es un
imbécile » que peuvent dire, dans des
circonstances analogues, certains
professeurs.
Mais ici, les mathématiques
remplissent également une autre fonction,
celle de représenter et d'exprimer leur moi
idéal considéré comme
précurseur et fondateur du sur-moi, cet
idéal de toute-puissance narcissique.
C'est en effet, grâce aux
mathématiques, que ces sujets vont avoir
l'impression de satisfaire leurs désirs
d'agressivité, de lutte, de jeu, et vont
trouver une image satisfaisante d'eux-mêmes :
plus forts que les autres, capables de faire
quelque chose. C'est grâce aux
mathématiques qu'ils ont ce sentiment de
trouver un monde où ils sont tout-puissants
et où l'angoisse ne surgit plus comme elle
le fait quand ils sortent de leur solitude pour
être au contact de leurs élèves
ou de leurs collègues.
C'est grâce à un
mécanisme de clivage que les
mathématiques peuvent à la fois jouer
le rôle de l'objet qui « résiste
», qui peut être un « obstacle
» et en même temps qui apporte cette
toute-puissance. Un exemple en a été
déjà donné dans l'entretien
« Jean-Pierre
et le trésor
mathématique
» dans lequel Jean-Pierre ressentait les
mathématiques à la fois comme un mur
qu'il voulait abattre pour ne pas se sentir
emprisonné, et à la fois comme un
trésor, un autre monde, pur, vierge,
où il se sentait à l'aise. « La
pensée mathématique réalise
à merveille cette évasion dans
l'imaginaire, mais un imaginaire sans danger,
contrôlable, manipulable, grâce par
exemple à des jeux de transformation
géométrique, à des changements
de coordonnées ou de variables où
s'exprime tout un maniement magique du réel,
par l'intermédiaire d'une pensée
imaginée toute-puissante. » (Lemaire,
p. 73.)
Il y a donc dans ce cas encore contact
avec le réel par l'intermédiaire des
mathématiques, mais distance du réel
dans la relation avec les autres objets. Il
peut s'agir parfois d'un simple «
rétrécissement de l'investissement
» pour échapper à l'angoisse et
à la culpabilité.
Dans cette catégorie C2, on peut donc
constater que les mathématiques peuvent
être mises au service du moi idéal
par le sujet, ce qui lui permet ainsi
: — de s'isoler
d'une partie de la réalité qu'il ne
supporte pas, tout en y adhérant, ne
serait-ce que par les
mathématiques. — de trouver
des satisfactions narcissiques dans un sentiment de
toute-puissance. — de se
constituer un sur-moi, tolérant certaines
pulsions particulièrement agressives, lui
assurant ainsi une zone de sécurité
où angoisse et culpabilité sont
tenues en échec. (Voir
l'Entretien
de Rosine) Catégorie
3
Cette classe fait apparaître la
représentation des mathématiques
comme être idéal ;
c'est-à-dire d'un être pourvu d'une
pensée dont le fonctionnement est parfait,
d'une pensée ordonnée, atteignant la
« Vérité » ; d'un
être sans faille, beau, harmonieux,
unifié et enfin d'un être pourvu de
toute-puissance. L'objet mathématique
devient alors ici objet de projection du
narcissisme primaire et expression de
l'idéal du moi du sujet. La
négation de tout manque se retrouvera dans
la relation aux élèves : le refus de
« toute opposition » et le désir
de « connaître » les
élèves traduira le désir de
combler toute apparition de faille.
C'est une représentation des
mathématiques comme pensée parfaite
et en particulier comme « ordre ». Ce
n'est plus l'ordre contraignant exprimé dans
l'étude de la classe C1 ce ne sont plus les
mathématiques mauvais objet contre lequel il
faut lutter. Ce n'est pas non plus l'ordre
exprimé dans l'étude de la classe
suivante C4, manifesté par des
qualités qu'il faut introjecter pour aider
son propre moi à lutter contre certaines
pulsions. Il s'agit ici, dans la classe C3, d'un
odre idéal vers lequel il faut tendre,
un « fil conducteur de la vie », comme le
dira un professeur au cours d'un entretien, une
vérité indispensable pour la vie. La
vérité existe et certains professeurs
de mathématiques en ont fait
l'expérience, grâce aux
mathématiques : « Il n'y a qu'en
mathématiques que je puisse être
sûr de la vérité » (q.
112). Elle régit les mathématiques
elles-mêmes (q. 101) et elle peut être
atteinte (q. 97). Ce que peut procurer la
possession de cette vérité, c'est la
« certitude », c'est « être
sûr » (q. 112) ; on trouve encore «
je suis sûr » (q. 101), « je sais
» (q. 97).
Dans les mathématiques, ce qui
intéresse le professeur, c'est « une
certaine forme de fonctionnement de la
pensée » (q. 86), c'est-à-dire
cette forme de fonctionnement parfait qui
doit donner la vérité : les
élèves n'ont pas cette
vérité il faut qu'ils la
reçoivent.
On peut encore rencontrer une telle attitude
chez certains mathématiciens qui
désirent arriver à une formulation
absolue de leurs énoncés pour obtenir
une vérité irréfutable et
incontestable. (Voir: Thom)
Dans toutes ces attitudes, que demande-t-on
aux mathématiques ? d'être le
garant d'une pensée idéale vers
laquelle on doit tendre
L'homme ne peut renoncer complètement
à la perfection du narcissisme de son
enfance, il recherche donc de différentes
façons cette perfection dans les objets
qu'il constitue en son idéal du moi. Les
mathématiques sont ainsi le support de la
projection de cette perfection narcissique et le
mathématicien ne vise à rien d'autre
que de tendre vers cet idéal pour retrouver
cette perfection paradisiaque.Tendre toujours
davantage vers cet idéal de
vérité peut avoir, parfois un
rôle de maturation.
Mais si l'idéal du moi pousse le moi
à réaliser toutes ses
intégrations, il semble qu'ici il s'agisse
tout particulièrement de pulsions de
maîtrise telles que «absence de
désordre ». On est donc en
présence d'un désir de parvenir
à un état « sans contradictions
», de « certitude » où toute
question possède sa « bonne
réponse ». « Bien faire »
devient « Bien raisonner
».
Ce n'est pas la problématique des
classes C 1 ou C4 où l'ordre est en quelque
sorte obligatoire ; il s'agit ici de l'atteindre
par amour ou plus exactement de le respecter le
mieux possible pour garder l'amour de
l'idéal du moi et la quiétude de
savoir que l'on est dans la
vérité.
Il existe donc
pour ces professeurs une intolérance aux
contradictions et aux incertitudes dont les
élèves font parfois les frais (q.
21).
Cet être idéal que
représentent les mathématiques ne
possède pas seulement une pensée
parfaite permettant d'atteindre la
vérité. Il possède
également la beauté, l'harmonie, la
puissance.
La beauté des
mathématiques est le thème de la
question 84 : beauté, harmonie ; c'est
également le thème de la question 89
: objet qui provoque éblouissement et
émerveillement. D. Nordon (Université
de Bordeaux) a effectué une enquête
auprès de 46 chercheurs de son
université. François Le Lionnais a
fait une étude sur « la beauté
en mathématiques » dans laquelle il
distingue deux genres de beauté, une «
beauté classique » et une «
beauté romantique » ; pour exprimer
l'opposition entre les deux, il utilise cette
phrase : « Elle se réduit
essentiellement ici à l'opposition entre
volonté d'équilibre et nostalgie du
vertige. » (Le Lionnais) et il termine son
article ainsi : « C'est ainsi que la
beauté se déploie en
mathématiques comme dans les autres
sciences, comme dans les arts, comme dans la vie,
comme dans la nature. Parfois comparable à
celle de la musique pure, de la grande peinture ou
de la poésie, les émotions qu'elle
éveille sont le plus souvent d'une nature
différente qui ne peut guère se
comprendre lorsqu'on n'en a pas ressenti en
soi-même l'illumination. La beauté des
mathématiques ne garantit certes ni leur
vérité, ni leur utilité. Mais
elle apporte aux uns le pouvoir de vivre des heures
incomparables, aux autres, la certitude que les
mathématiques continueront à
être cultivées pour le plus grand
profit de tous et la plus grande gloire de
l'aventure humaine par des hommes qui n'en
espèrent pour eux-mêmes aucun profit
matériel ».
Les mathématiques sont bien ici un
objet idéal dont la beauté, faite de
la volonté d'équilibre et de la
nostalgie du vertige, en est une des
parures.
L'unité est une autre parure des
mathématiques. « Je trouve du
plaisir en mathématiques à aller de
la diversité à l'unité »
(q. 115).
La dernière parure
attribuée aux mathématiques est ce
pouvoir qu'elles donnent à celui qui
exerce cette discipline : « jeu où l'on
a toutes les données en main » (q. 92),
moyen de surmonter les obstacles (q. 85),
possibilité de bien raisonner (q. 113). Ce
thème est justement l'un de ceux qui
existent dans la représentation
sociale.
On peut résumer tous ces
thèmes : les mathématiques
paraissent pouvoir apporter à celui qui les
pratique un objet beau, harmonieux, unifié,
tout-puissant. Cet objet provoque
l'éblouissement, l'émerveillement, la
nostalgie du vertige, un sentiment d'unité
et de puissance, autrement dit la plénitude
de l'être.
L'idéal du moi peut fonctionner ici
comme idéalisation du propre moi, d'un moi
beau, équilibré, c'est-à-dire
sans conflits, sans chaos, raisonnant bien
(c'est-à-dire ne dé-raisonnant pas)
et possédant la puissance.
Ce mode de relation où la
négation du manque et le désir de
combler l'autre prédominent va se retrouver
dans la relation aux élèves.
T
oute « opposition » de la part des
élèves (q. 21) est rappel de ce
manque. Il n'y a pas plus de possibilité de
satisfaire tous les élèves qu'il n'y
en a de satisfaire la mère. C'est
pourquoi« ne pas connaître ses
élèves aussi bien qu'un professeur de
français » (q. 22) provoque un «
regret ». Inversemenent le professeur
cherchera à renforcer ce désir de
combler l'élève, c'est pourquoi il
aime que ses élèves viennent lui
parler de « leurs problèmes personnels
» (q. 16), il est « à
côté d'eux » (q. 18), mais il
semble que ce rapprochement ne soit que verbal
puisque le « contact physique » est
évité (q. 35). L'aspect narcissique
de l'attitude du professeur apparaît encore
dans le plaisir qu'il éprouve à
« faire un peu de théâtre en
classe pour intéresser les
élèves (q. 33).
Dans tous ces cas, même lorsqu'il
cherche à vérifier « tout »
le travail de ses élèves (q. 11),
il est celui qui peut combler le désir de
l'autre. (Voir:
Pascale
ou la machine à distribuer les
maths)
Cette idéalisation de l'objet
mathématique peut parfois conduire à
ce qu'il soit considéré comme un
véritable objet anaclitique dans la mesure
où le surinvestissement de cet objet est
tel que le sujet devient entièrement
dépendant de sa relation à cet
objet. On lira l'entretien «
Jean-Pierre
et le trésor
mathématique
» : dans celui-ci, cet élève
parle de se suicider s'il n'arrivait plus à
suivre en mathématiques.
Dans un entretien, un professeur
de
mathématiques
nous disait « il n'y a que les maths dans ma
vie », que les mathématiques sont le
« tissu de ma vie », la « trame de
fond », qu'elle était «
greffée sur les mathématiques ».
L'angoisse sous-jacente est celle de la perte de
cet objet, de ce qu'il représente et de la
dépression qui peut s'en suivre.
Chez certains, l'idéal
représenté par les
mathématiques est plus large : «
bien raisonner » ne suffit pas. Ce qui est
alors recherché, c'est une complétude
faite de beauté, d'harmonie, d'unité
et de puissance. Les maths serviront alors à
combler, en partie, la blessure narcissique que
tout individu conserve. Une telle utilisation des
mathématiques a déjà
été décrite, chez les
élèves, dans le mécanisme de
retournement en son contraire (vaincu-vainqueur).
Pour d'autres encore, cet objet
mathématiques aura une fonction de
fétiche en tant que dénégation
du manque : dénégation du manque
d'harmonie, c'est-à-dire de la
présence de conflit en soi,
dénégation du manque d'unité
en soi, enfin dénégation de la
non-toute-puissance. L'objet mathématique
aura alors une fonction de marque ou de masque du
manque qu'il souligne en le déniant, qu'il
reconnaît en le désavouant
Il n'est donc pas étonnant que ce
genre de professeurs soit « très
attentif» aux « manques » de leurs
élèves. Cela peut expliquer parfois
pourquoi ils préfèrent les «
bons élèves » auprès
desquels ils peuvent trouver par reflet une image
d'eux-mêmes rassurante. J'ai toujours
été surpris par la différence
« d'intérêt » qu'il m'a
semblé percevoir chez certains enseignants
du secondaire et chez des
rééducateurs (orthophoniste, etc.).
Les uns paraissent fonder leur travail sur le
désir d'absence de manque chez leurs
élèves, les autres sur leurs propres
manques. Catégories
C4
Les questions de la classe C4 peuvent
être interprétées comme
l'expression, soit d'un processus
d'intellectualisation ayant pour but de
maîtriser et à la limite de refouler
des pulsions interdites, soit un processus de
symbolisation ayant pour but d'aider à
la structuration du moi et plus
généralement de la
personnalité.
La question 91 « Ce que j'aime dans les
mathématiques, c'est leur rigueur »
permet de se rappeler que les mathématiques
sont souvent associées à l'ordre,
à la rigueur morale (cf. l'entretien :
« Jean-Pierre
et le glissement de
signifiée»).
La recherche de la rigueur s'allie à la
recherche de la maîtrise, maîtrise des
symbole mathématiques « En
mathématiques, j'ai souvent le plaisir de
voir les choses se mettre en place et s'organiser
» (q. 87) et maîtrise de la classe
« Je donne des devoirs
régulièrement pour contrôler
mes élèves » (q. 29) ainsi que
« J'envoie mes élèves à
tour de rôle au tableau » (q. 10) et
« J'interdis à mes élèves
de fumer pendant mes cours » (q.
12).
Derrière cette recherche de
maîtrise des mathématiques et de celle
de la classe, on peut percevoir un désir de
maîtrise de ses propres pulsions et tout
particulièrement des pulsions
agressives. La question «
Je trouve important de faire sentir à mes
élèves qu'on peut se servir de sa
pensée » (q. 27) est l'expression,
justement, de cette prédominance que l'on
attribue à la pensée sur l'affect.
J'interpréterai ainsi ces questions : elles
expriment l'utilisation des mathématiques
comme une modalité de la loi symbolique
ayant pour fonction de structurer le moi. En effet,
dans la mesure où les mathématiques
sont un code universel, elles peuvent être
une expression de la loi symbolique.
C'est ainsi que l'on peut comprendre qu'un
professeur de mathématiques aime des
mathématiques « cohérentes
», « rigoureuses », «
organisées », «
précises», pour lui-même et pour
en faire bénéficier ses
élèves : il y trouve un sentiment
« d'unité », « d'organisation
», de construction, non seulement dans les
mathématiques elles-mêmes, mais pour
lui-même, par leur introjection. C'est la
construction de son moi, de sa maîtrise, de
son unité, qu'il a « l'impression
» d'entreprendre à travers cette
activité ; et dans la mesure où
effectivement les mathématiques sont un
représentant de la loi symbolique, on peut
penser qu'il s'agit bien d'une structuration du
moi.
Cette structuration du moi peut se
faire, me semble-t-il, de deux façons :
par introjection « Le sujet fait passer,
sur un mode fantasmatique du "dehors" au "dedans"
des objets et des qualités inhérentes
à ces objets » (Laplanche et Pontalis,
loc. cit., p. 209). Les sujets trouvent alors les
mathématiques « cohérentes
», « unifiées », «
solides ». C'est après avoir
projeté ces qualités sur les
mathématiques qu'ils les introjectent dans
leur moi pour acquérir cohérence,
unité, solidité. On peut aussi
envisager un autre processus qui peut exister aussi
chez les sujets classés dans le groupe C3.
On voit ici la limite d'un tel découpage.
Ce processus est décrit par Lacan
dans le stade du miroir. « L'enfant encore
dans un état d'impuissance et
d'incoordination motrice, anticipe imaginairement
l'appréhension et la maîtrise de son
unité corporelle. Cette unification
imaginaire s'opère par identification
à l'image du semblable comme forme
totale ; elle s'illustre et s'actualise par
l'expérience concrète où
l'enfant perçoit sa propre image dans un
miroir. Le stade du miroir constituerait la matrice
et l'ébauche de ce qui sera le moi. »
(Laplanche et Pontalis, loc. cit., p. 452). Les
mathématiques seraient ici cet objet dans
lequel se mirerait le professeur, et dans lequel il
pourrait voir son « unité » et sa
« cohérence » ".
Que ce soit par des mécanismes
défensifs de refoulement ou
d'intellectualisation, que ce soit par introjection
« d'un bon ordre »
représentant de la loi symbolique ou par une
identification à un objet jugé comme
« total », dans tous les cas les
mathématiques ont pour fonction de
rigidifier, de renforcer ou de structurer le moi de
façon plus ou moins bien adaptée. Les
mathématiques sont ici au service du
moi.
Or, il existe chez les élèves
un mécanisme que j'avais appelé
introjection d'un bon ordre, utilisé
tout particulièrement par les
élèves de séries scientifiques
et qui leur assure une certaine
sécurité. (Voir chez
les
élèves).
On conçoit que les mathématiques,
avec leurs règles, avec leur langage qui ne
souffre pas l'ambiguïté, puissent
être particulièrement propices
à ce type d'investissement ; derrière
cette recherche de maîtrise se profile
souvent une agressivité dont bien des
élèves font les frais. Lorsque le
professeur recherche avant tout la réussite
de ses élèves, il manifeste surtout
la préoccupation d'une certaine
réussite de lui-même, d'une
construction de son moi. Répondez
au sondage puis passez à la
suite: Conséquences
pédagogiques des diverses
représentations des
mathématiques
chez
les enseignants de cette
discipline
|