|

PLAN
DU SITE
|
ETHNOLOGIE ET NOMBRE
|
thèse
soutenue par: Benoît
MAURET dans
l'U.E.R. de Sciences de
l'Éducation de PARIS V sous la
direction du Professeur
Gérard VERGNAUD .
Nous en
donnons ici des extraits et des
synthèses qui sont
évidemment choisis de façon
subjective.
|
|
|
|
PERCEPTION
NATURELLE DES NOMBRES.
|
<<Chez
l'homme comme chez l'animal le sens du nombre est
très limité. Sans avoir recours au
mécanisme de comptage qui nous est devenu
tellement familier, la perception des nombres ne
dépasse pas souvent le chiffre 4.
Lorsque nous avons une collection de plusieurs
objets identiques nous ne pouvons percevoir
directement la quantité. La sensation
numérique directe est vite limitée et
il devient nécessaire d'utiliser les
schèmes du dénombrement.
Tobias Dantzig souligne que le sens du
nombre n'est guère plus
développé chez l'homme que chez les
animaux :
«Des
expériences menées avec le plus grand
soin ont conduit à la conclusion
irréfutable que le sens direct visuel du
nombre, chez un homme cultivé moyen,
dépasse rarement le nombre 4 et que le sens
tactile est encore plus
limité».
Ce résultat est confirmé par
L. Gerschel qui montre la difficulté de
«lire» d'un seul coup d'oeil une suite de
cinq traits 11111 ou de six traits Cela devient
encore plus difficile pour des quantités
plus importantes.
Les études anthropologiques
confirment ces limites de la perception visuelle.
Pour certaines tribus d'Australie, d'Afrique et
d'Amérique du sud il n'existe pas de noms de
nombres autre que un, deux et beaucoup. Selon
Tobias Dantzig ce même
phénomène se retrouve dans la langue
Anglaise où le mot thrice comme le latin ter
a deux sens «trois fois» et
«beaucoup»>>(p.11)
|
<<Des
observations anthropologiques ont
confirmé l'usage limité des
nombres chez de nombreuses tribus.
Selon A. Sommerfelt la tribu
australienne Aranda n'utilisait au
début du siècle que deux
noms de nombre
-
ninta pour un et tara pour la paire.
Pour
désigner trois ils composaient un
et deux : tara-mi-ninta (deux et un).
Au-delà
de quatre ils utilisaient le mot
"beaucoup".>>(p.13)
|
|
|
DIFFÉRENTS
PROCESSUS DE COMPTAGE
EN
RELATION AVEC L'OBJET
CORPS.
|
Processus
d'appariement.
<<Pour
remédier aux limites de la perception
immédiate des nombres et pour compter des
quantités d'objets importantes l'homme dut
faire appel à des techniques
numériques. Sans avoir pour autant atteint
le stade de la conception abstraite du nombre il a
su compter depuis de nombreux siècles. Nous
observons que l'expérience de techniques
numériques a précédé et
permis la genèse du concept de nombre .
Le procédé alors utilisé
est la comparaison terme à terme .Il
s'agit du concept d'appariement que l'on
désigne en mathématique sous le nom
de relation bijective.>>(p.14)
Appariement avec
le corps humain'
<<D'un
emploi immédiat et facilement disponible
les éléments du corps humain ont
très tôt constitué un
référent pour procéder aux
techniques de la correspondance terme à
terme . Nous retrouvons cet usage dans des
observations ethnologiques pour des pays
différents. Dans son ouvrage
Lévy-Bruhl rapporte beaucoup d'exemples
illustrant ces techniques de
dénombrement>>(p.15)
|
Un
premier exemple:
<<Dans
ces travaux sur ce peuplement le docteur
Wyatt Gill écrit: «au-dessus
de dix les insulaires du détroit de
Torrès comptent visuellement de la
façon suivante :
|
on touche
les doigts un à un, puis le
poignet, le coude et l'épaule du
côté droit du corps, puis le
sternum, ensuite les articulations du
côté gauche, sans oublier les
doigts de la main gauche. On obtient ainsi
17. Si cela ne suffit pas on ajoute les
doigts du pied, la cheville, les genoux et
les hanches (à gauche et à
droite). On obtient ainsi 16 de plus, donc
33 en tout. Au-delà de ce nombre,
on s'aide d'un paquet de petits
bâtons.»>>(p.15)..
|
|
<<Un
deuxième exemple
nous est
donné par la langue Papoue du
nord-est de la Nouvelle-Guinée.
Selon W. Mac Gregor on observe une
technique gestuelle dans les villages sur
la rivière Musa : «on commence
par le petit doigt de la main droite, on
emploie les doigts de ce
côté, puis le poignet, le
coude, l'épaule, l'oreille et
l'oeil de ce côté, de
là on passe à l'oeil gauche
etc ... On redescend jusqu'au petit doigt
de la main gauche. Beaucoup
d'indigènes s'embrouillent en
comptant quand ils arrivent à la
figure».
Au constate que le même terme
doro correspond à 6 doigts
différents. Cela illustre bien que
les termes employés ne sont pas des
noms de nombres car sans le geste
correspondant il pourrait se produire des
confusions.>>(p.17)
|
Ainsi
ils utilisent le dénombrement
suivant
1 Anusi :
petit doigt de la main droite.
2 3 4
doro.
5 Ubei
pouce droit.
6 Tama
poignet droit.
7 Unubo :
coude droit.
8 Visa :
épaule droite.
9 Denoro -
oreille droite
10 Diti
oeildroit.
11 Diti
oeil gauche
12 Medo :
nez.
13 Bec:
bouche.
14 Denoro
: oreille gauche.
15 Visa :
épaule.
16 Unubo :
coude.
17 Tama
poignet.
18 Ubei
pouce.
19 20 21
Doro.
22 Anusi :
petit doigt de la main
gauche.
|
|
Le
troisième exemple
nous est
donné par Hautrey dans son ouvrage
«The number concept chez les indiens
Lengua du Chaco au Paraguay>> Cet
exemple est également cité
dans l'ouvrage de Lévy-Bruhl. Pour
les 20 premiers nombres nous avons les
noms suivants:
Ainsi les indiens du Chaco
utilisent également une
série déterminée de
termes concrets où il apparait que
les nombres ne sont pas
différenciés du corps
humains.
|
1 Thlama-2
Anit-3 Antanthlama (composé de un
et deux)-4 Les deux côtés
pareils-5 Une main-6 Arrivé
à l'autre main, un-7 Arrivé
à l'autre main, deux-10 Fini les
deux mains-11 Arrivé au pied, un-16
Arrivé à l'autre pied, un-20
Fini les pieds.
Au
delà on dit "beaucoup" et s'il
s'agit d'un nombre très
élevé on fait appel aux
"cheveux de la tête".
|
|
|
A l'aide de ces différents
exemples on s'aperçoit que
l'étymologie des noms de nombres
révèle très fréquemment
une technique corporelle de comptabilité. Ce
phénomène peut s'observer pour des
civilisations très différentes et
très éloignées
géographiquement. Cependant on peut
comprendre les limites d'un tel
procédé car la seule
énumération des parties du corps ne
suffit pas à désigner un nombre
précis. Il est nécessaire de
l'accompagner d'un geste. Pour remédier
à cette faiblesse les hommes ont dû
élaborer une suite ordonnée de mots
désignant les différents nombres et
permettant un dénombrement oral
accompagné d'un appariement devenu
visuel.>>(p.18-19)
|
|
LES
BASES NUMÉRIQUES ET
LEUR
RAPPORT AVEC LE CORPS
HUMAIN.
|
<<Afin de
limiter le nombre de symboles numériques
distincts l'homme construisit un système de
numération approprié , la
base. Il s'agissait de répondre
à deux nécessités :
- La
première, reposant sur le principe de
cardinalisation, consiste à
répéter un symbole étalon
représentant l'unité.
- La
deuxième, reposant sur le principe
d'ordinalisation, consiste à
représenter chaque nombre par un symbole
différent.
Nous pouvons nous
interroger sur la diversité des modes de
numération utilisés . Comment la
relation établie avec le corps humain a
conduit l'homme vers le choix d'une base
plutôt qu'une autre ?
Base
dix.
Nous avons déjà observé
que pour la structure des noms de nombres les
dix doigts de la main avaient joué un
rôle important. De même nos dix
doigts ont influencé très fortement
le choix de la base de numération. Tobias
Dantzig écrit
«Dans toutes
les langues indo-européennes, aussi que dans
les langues sémites, mongoles et dans la
plupart des idiomes des races primitives, la base
de la numération est dix, autrement dit, il
existe des noms de nombres distincts jusqu'à
dix; au-delà il existe partout quelque
système pour atteindre cent sans mots
nouveaux.»
Le fait que le
système décimal soit largement
répandu confirme la nature anthropomorphique
de notre façon de compter. Ce choix
imposé par la structure de notre propre
corps n'était pas le plus judicieux. Pour
avoir davantage de diviseurs et plus de
commodités les scientifiques auraient
préféré le choix de la base
douze. Encore de nos jours dans la vie quotidienne
on trouve l'usage d'un compte en base douze : une
douzaine d'oeufs, une douzaine d'huîtres,
etc...
Base
cinq,
Comme choix de base on rencontre
également la base quinaire : base cinq. Il
s'agit d'une prédominance du groupement par
cinq. Ce système s'observe quand les cinq
premiers noms de nombres sont distincts tandis que
pour les noms suivants on se contente de mots
composés. Un premier exemple nous est
donné par Georges lfrah. Il s'agit d'une
technique digitale employée encore de nos
jours par les habitants de Bombay. Dans ce
procédé la main gauche
désigne les unités tandis que
la main droite désigne des
groupements de cinq
unités>>(p.20-21)
Base
vingt
<<Certains
peuples avaient adopté vingt comme base pour
compter. De la même façon que pour dix
le choix de la base vingt révèle une
origine anthropomorphique. Il nous reste des
témoignages de l'usage du système
vicésimal. En particulier G. Ifrah cite le
cas de la langue Aztèque où l'on
s'aperçoit que les vingt premiers nombres
correspondent aux dix doigts des mains et aux
dix doigts des pieds.>>(p.22)
Base
2.
<<Dans son
livre Tobias Dantzig cite les travaux de Curr sur
les tribus d'Australie. Ces peuples n'ont pas
encore atteint le stade de compter sur les doigts
et le système qu'ils emploient est
binaire : «Ils ont des vocables
indépendants pour désigner un et
deux, ensuite ils emploient des noms
composés jusqu'à 6, au delà
ils emploient un mot qui veut dire
tas».>>(p.24)
|
|
<<L'histoire
nous montre qu'il a fallu attendre le
douzième siècle pour que la base dix
se généralise de plus en plus.
Pour les unités de mesure il a fallu
attendre encore plus longtemps car c'est seulement
en 1790 que le gouvernement révolutionnaire
a généralisé le système
décimal à la plupart des mesures. Les
unités anciennes révélaient
l'importance de la base 5, 12, 20 et aussi les
survivances de techniques de numération
digitale. Dans les unités de longueur
l'homme avait communiqué son "unité
corporelle aux différentes
unités
1 toise = 6
pieds
1 pied = 12 pouces
1 pouce = 12 lignes 1 ligne = 12 points.
Enfin une livre
valait 20 sous et un sou valait 20
deniers.
A travers ces différentes
unités de mesure on observe bien la
prégnance de la base 12 et de la base 20.
Ainsi dès l'origine de notre système
de numération nous pouvons comprendre
comment l'homme utilise les représentations
de son propre corps pour élaborer la
connaissance. L'exemple de la numération
est particulièrement riche car sa
genèse remonte très loin dans le
temps (le plus ancien document de
dénombrement connu est un os de loup
daté de 30.000
ans).>>(p.25)
|
|
L'origine de la
dactylonomie et son
développement.
<<De nombreux
documents anciens laissent envisager que
l'Égypte serait à l'origine du
compte manuel. Dans son ouvrage G. lfrah cite
des documents qui pourraient témoigner de
cette origine. En effet on peut observer sur les
fresques d'un monument Égyptien de l'ancien
empire (5ème dynastie 26 siècle av.
J.C) des ouvriers mesurant du grain avec des
boisseaux et des comptables opérant avec
leurs doigts et dictant les résultats
à des scribes.>>(p.26)
|
Compte
utilisant les phalanges et les jointures
des doigts
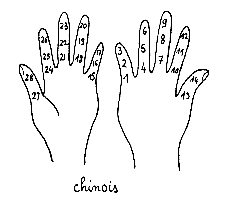
<<En
extrême Orient on peut encore de nos
jours trouver une technique du compte
digital faisant intervenir les phalanges
ou les articulations du doigt. G. lfrah
cite dans son livre une pratique
couramment utilisée en Chine et en
Indochine : «Dans ce
procédé (qui se pratique sur
chacune des deux mains à l'aide
d'un doigt de l'autre), chaque phalange de
la main compte pour une unité, en
commençant par la phalange
inférieure du petit doigt pour
finir par la phalange supérieure du
pousse de la même main». En
utilisant ce procédé on peut
aller jusqu'à 28 sur les deux
mains.>>(p.34)
|
|
Opérations
utilisant une technique digitale.
<<Survivant
après des siècles nous pouvons
observer des procédés de
multiplication avec les doigts.
Table de
multiplication par 9.
Nous pouvons observer pour les
élèves ayant des difficultés
à mémoriser la table de
multiplication une technique digitale donnant
immédiatement le résultat par lecture
directe sur les doigts de la main. Quelques
élèves l'utilisent
discrètement en classe. Nous n'avons pas
trouvé dans la littérature sur les
techniques digitales des traces de ce processus
mnémotechnique.
|
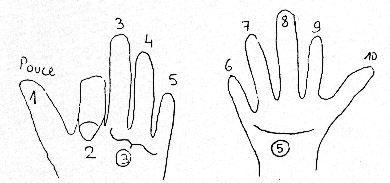
La
technique utilisée est la
suivante
Pour 0
< X < 10
9 fois X
exemple : 9 * 2 = ?
On abaisse
le deuxième doigt de la main gauche
et on lit sur les deux mains face à
soi-même. Le nombre de doigts se
trouvant avant le doigt replié
désigne les dizaines. Dans ce cas
nous avons une dizaine. Les doigts
à droite du doigt replié
désignent les unités. Soit 3
+ 5 - 8 unités et par
conséquent on obtient la lecture
directe : 9 * 2 = 1( ) 8 donc 9 * 2 =
18.
|
|
|
Autre
exemple,
9 * 8 =
?
On abaisse
le huitième doigt, ainsi on obtient
7 doigts avant le doigt
replié.
Soit 7*
10=70
Deux
doigts après le doigt replié
soit 2 unités 9 * 8 = 70 + 2 =
72.>>(p.36-37)
|
|
|
SIGNIFIANTS
NOMBRES ET
ANTHROPOMORPHISME.
|
<<Pendant
des millénaires l'homme a
représenté les nombres à
l'aide des différentes parties du corps :
mains, pieds, articulations, etc... Ces techniques
de compte corporel étaient limitées
par le fait qu'elles ne permettaient pas une
mémorisation durable.
Il a fallu se donner des outils pour
conserver les traces de quantités
dénombrées et avoir ainsi des
résultats toujours disponibles....Un peu
plus tardive mais presque contemporaine est apparue
l'écriture égyptienne (3000 av. J.C).
La numération hiéroglyphique nous
donne un exemple de projection anthropomorphique.
Basée sur les puissances de 10 elle repose
sur le principe d'addition. Deux signifiants
employés correspondent au monde
végétal : (fleurs de lotus) tandis
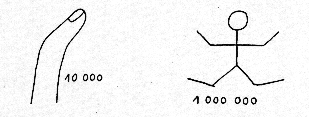
que deux autres évoquent le corps humain.
Le nombre 10.000 est représenté
par un doigt relevé,
légèrement
incliné.
Le nombre 1.000.000 est
représenté par un homme
agenouillé et levant les bras vers le
ciel. (voir dessin en haut de la page). Ce
dernier nombre symbolisait également
l'éternité et l'infini. Ce doigt
dessiné serait-il une survivance et un
témoignage du compte digital ?. De
même les bras levés sur la tête
évoquent les gestes des peuples Africains
pour désigner une quantité
indénombrable.>>(p.42-43)
|
|
<<L'histoire
des nombres nous montre combien est difficile
l'objectivation de la pensée humaine. Durant
les différentes étapes de
l'élaboration de la suite numérique
l'homme a utilisé son corps comme un support
concret permettant dans un premier temps
l'appariement et dans un deuxième temps un
dénombrement limité.
A travers le rapport à son propre
corps l'homme a ainsi facilité l'apparition
de certaines bases privilégiées comme
la base 5, la base 10, la base 20. Cette projection
se retrouve également dans la construction
de signifiants graphiques en particulier elle
apparaît dans le système de
numération des Égyptiens. Par
conséquent comme le souligne
Lévy-Bruhl (A . )
«Les
numérations comme les langues dont on ne
doit pas les séparer sont des
phénomènes sociaux qui
dépendent de la mentalité
collective».
Ainsi dès
leur origine les nombres ont servi de support aux
fantasmes, à la magie et aux intuitions
métaphysiques.
|
Ce
rapport au corps humain nous montre
comment
la
subjectivité et
l'affectivité
peuvent
pénétrer l'univers
même des
nombres.
|
|
|
D'autre part la genèse du
dénombrement nous conduit à penser
que le concept de nombre est davantage le
résultat d'une expérience
sensori-motrice que d'une représentation
déjà construite. Si le concept
"outil" a précédé le concept
"objet" pour les nombres, nous pouvons cependant
réfuter cette hypothèse pour les
chiffres 1 et 2 par le fait qu'ils font partie de
l'environnement proche et familier de
l'homme.
Une présentation historique des
nombres peut apporter de nombreux avantages pour la
didactique des mathématiques. En particulier
elle permet de lever des obstacles et de donner du
sens à de nombreux concepts.
Ces mêmes nombres si souvent
associés à des symboles arides et
dépourvus de sentiments dans les
sociétés fortement technologiques
sont tout au contraire riches d'un passé
mêlé au devenir humain.
Comme Georges lfrah, nous soulignerons notre
émerveillement et notre fascination pour
l'univers des nombres : «les chiffres sont une
substance poétique ...
»>>(p.46-47)
|
|
Réaction
|
<<Cet extrait
de thèse apporte de nombreux
éclairages quant à la
réflexion que je mène sur le nombre.
Un très grand merci à son
auteur.>>
<<Passionnante,
cette étude; certains exemples de
dénombrement sur le corps pourront
même me servir dans la classe maternelle
(j'avais appris en son temps la table de 9 et avait
bien remercié mon instit de ce "truc"
Cordialement>> EL
<<Bonjour,
je suis très interessé par le sujet.
Juste deux questions: Qu'est ce qu'un nombre?
Pourquoi ne parlez-vous pas de la genèse du
nombre? Enfin existe il une relation entre nombre
et lettre. et si oui laquelle.>>
|
|



