|
La
"lógica matemática"
Todos nuestros
razonamientos están basados en la
"lógica". ¿Pero de qué
lógica se trata? ¿De la lógica
matemática que uno aprendió en el
colegio: lógica de aserciones verdaderas o
falsas a las que uno hacía corresponder 1 o
0, para deducir de ellas la verdad de otras
aserciones? ¿Se trata de lógica
encontrada en física en donde a cada
"efecto" correspondía una
"causa"?
Pero estas
lógicas se han vuelto cada vez más
complejas, como lo explica Alain
Bouvier:
|
|
"La
tradición racionalista
cartesiana llevaba a considerar, entre
dos objetos o dos entidades A y B,
esencialmente relaciones de tipo "Causa
/® / Efecto", irreversibles,
buscando traer todo efecto discernido a
una causa: A® B.
A la
imagen de la equivalencia "trabajo "
calor" de la termodinámica, el
acercamiento sistémico considera
que una acción de A sobre B
siempre está acompañada
de una acción de vuelta de B
sobre A, y que para su análisis
importa tomarlas en cuenta a las dos.
Así, un foso separa (o parece
separar) al racionalismo cartesiano del
pensamiento sistémico, que busca
describir formas de causalidad
más elaboradas (circular, en
espiral…) y, lo veremos, discernir
vínculos entre varias causas y
varios efectos."
|
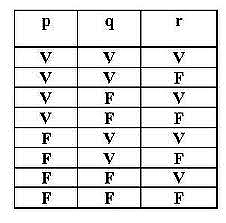
Hasta la
lógica matemática se complica,
basándose ya no solamente en aserciones
"verdaderas" (1) o "falsas" (0), sino considerando
aserciones que tienen una cierta probabilidad "p"
de ser "verdaderas" (0 £ p £ 1) en una
lógica llamada "borrosa".
Estas
consideraciones nos incitan ya a enriquecer nuestra
visión de la pedagogía. Nos permiten
comprender que un alumno necesita revisar varias
veces en una lógica circular los mismos
conceptos que se enriquecerán en cada pasaje
con todo lo que será adquirido entre
tanto; admitimos mejor que un programa pueda
contener varias partes similares y que la
linealidad de exposición o de lectura de un
libro, por ejemplo, no sea siempre el mejor
procedimiento…
La lógica
de las "asociaciones de ideas"
Pero existe
otra lógica: la de las "asociaciones de
ideas", la cual permite pasar de una
representación a otra y construir así
"cadenas asociativas" propias a una persona.
Tomemos la comparación siguiente: una
carreta jalada por un caballo sobre un camino llega
a un crucero, el conductor quiere girar a la
derecha, pero la carreta gira a la izquierda ya que
hay surcos, rieles que se han cavado a lo largo del
tiempo y que llevan a la carreta por el camino ya
trazado. Ocurre igual en nuestro cerebro, donde
nuestras neuronas han fijado caminos privilegiados
que desembocan en asociaciones personales.
Damasio escribe:
"Expliqué
en el capítulo 2 que el funcionamiento de
los circuitos neuronales depende de la
configuración de las conexiones entre
neuronas y del grado de acoplamiento entre las
neuronas, garantizado por las sinapsis al nivel
de las conexiones. En el caso de una neurona
excitadora, por ejemplo, las sinapsis "fuertes"
facilitan la propagación de los
potenciales de acción, mientras que las
sinapsis "débiles" actúan a la
inversa. Ahora, puedo añadir que la
fuerza de las conexiones sinápticas, en
el seno de numerosos sistemas neuronales y de un
sistema neural al otro, varía en
función de las experiencias vividas, y
que así la experiencia vivida juega un
papel en el modelado de los
circuitos."
Es esta
lógica la que prevalece a menudo en los
"errores" de los alumnos.
Es entonces
importante que el profesor se vuelva apto para
escuchar esas asociaciones de ideasa fin de dar la
información útil al alumno en lugar
de la repetición de una explicación
comodín.
Las
diferencias entre las dos
lógicas
La
lógica matemática es universal;
es decir que dos personas "razonables"
encontrarán los mismos resultados para un
problema dado.
La
"lógica de las asociaciones de ideas" es
personal; uno no puede asociar en lugar de
alguien más. Es por esto que no es posible
dar un sentido a un gesto o a una expresión
en lugar de su autor, sólo él puede
saber a qué lo remite ese gesto, esa
expresión, y seguir las cadenas asociativas
que le permitirán encontrar su propio
sentido. Hay un corte epistemológico, por
ejemplo, entre la manera de interpretar los
sueños en la época bíblica y
desde Freud. Antiguamente, la persona encargada de
interpretar el sueño tenía su
diccionario (todavía existen). Cada
término estaba descodificado: "7 vacas
gordas" = "7 años de abundancia", "7 vacas
flacas" = "7 años de hambruna". Desde Freud,
sólo aquel que soñó puede
encontrar las cadenas asociativas que construyeron
ese sueño de la manera más singular
posible.
La
lógica matemática nos hace parecernos
a los otros, es común a todos en su
agenciamiento.
La
"lógica de las asociaciones de ideas" es, al
contrario, lo que nos diferencia de los otros.
Es, dicho de otra manera, lo que hace que seamos
seres "únicos".
La
lógica matemática será
utilizada particularmente para demostrar, para
probar.
La lógica
de las asociaciones de ideas, principalmente
para descubrir, para crear considerando la realidad
de manera nueva, de manera única y en la
cual nadie había pensado.
Algunos hacen el
paralelo con la existencia de nuestros dos
cerebros, el cerebro derecho y el cerebro
izquierdo, y muestran que es de nuestro
interés aprender a servirnos de nuestros dos
cerebros.
Las
lógicas y la clase
|
Nuestra
enseñanza en Francia privilegia el
aspecto deductivo, el aspecto lineal. Un
profesor que comprende el interés
de las dos lógicas buscará
reequilibrar su
enseñanza.
La
utilización de los multimedia
plantea el problema de manera
todavía más crucial. Demanda
de los profesores hacer prueba de
más adaptabilidad, de más
creatividad y sobre todo de más
escucha.
|

|
Dicho de otra
manera, la técnica no resuelve los problemas
de la clase sino que los amplifica, lo que explica
la necesidad imperiosa de preparar
psicológicamente a los profesores para los
cambios de actitud impuestos por estas nuevas
técnicas; si no, se volverá a
producir lo que ocurrió cuando aparecieron
los televisores en las clases: terminaron
después de algún tiempo en los
hogares sociales culturales, o lo que
ocurrió después de la
formación "Informática para todos":
muchos computadores terminaron en los armarios.
¿Cómo preparar a los profesores?
¿Cómo, en particular, formarlos para la
escucha?
|



